Shashank Shekhar

Sharding

2 min read

Sharding

Sharding (also called partitioning) is the process of splitting arrays across multiple accelerators to enable distributed computation for models that exceed the memory capacity of a single device.

Key Concepts

Shapes of Sharded Arrays

  • Global/Logical Shape: The conceptual size of the complete array
  • Device Local Shape: The actual size stored on each individual device
  • Memory Reduction: Each device typically stores only 1/N of the total array (where N is the number of shards)

Device Mesh

A device mesh is a multi-dimensional grid of accelerators with assigned axis names:

  • Typically 2D or 3D arrangement (X, Y, Z axes)
  • The mesh defines the physical layout of the devices
  • Example: Mesh(devices=((0, 1), (2, 3)), axis_names=('X', 'Y'))

Named-Axis Notation

We use subscript notation to indicate how array dimensions are distributed:

  • A[I, J]: Fully replicated array (complete copy on each device)
  • A[IX, J]: First dimension sharded along X mesh axis
  • A[IX, JY]: First dimension sharded along X, second along Y
  • A[IXY, J]: First dimension sharded along both X and Y (flattened)

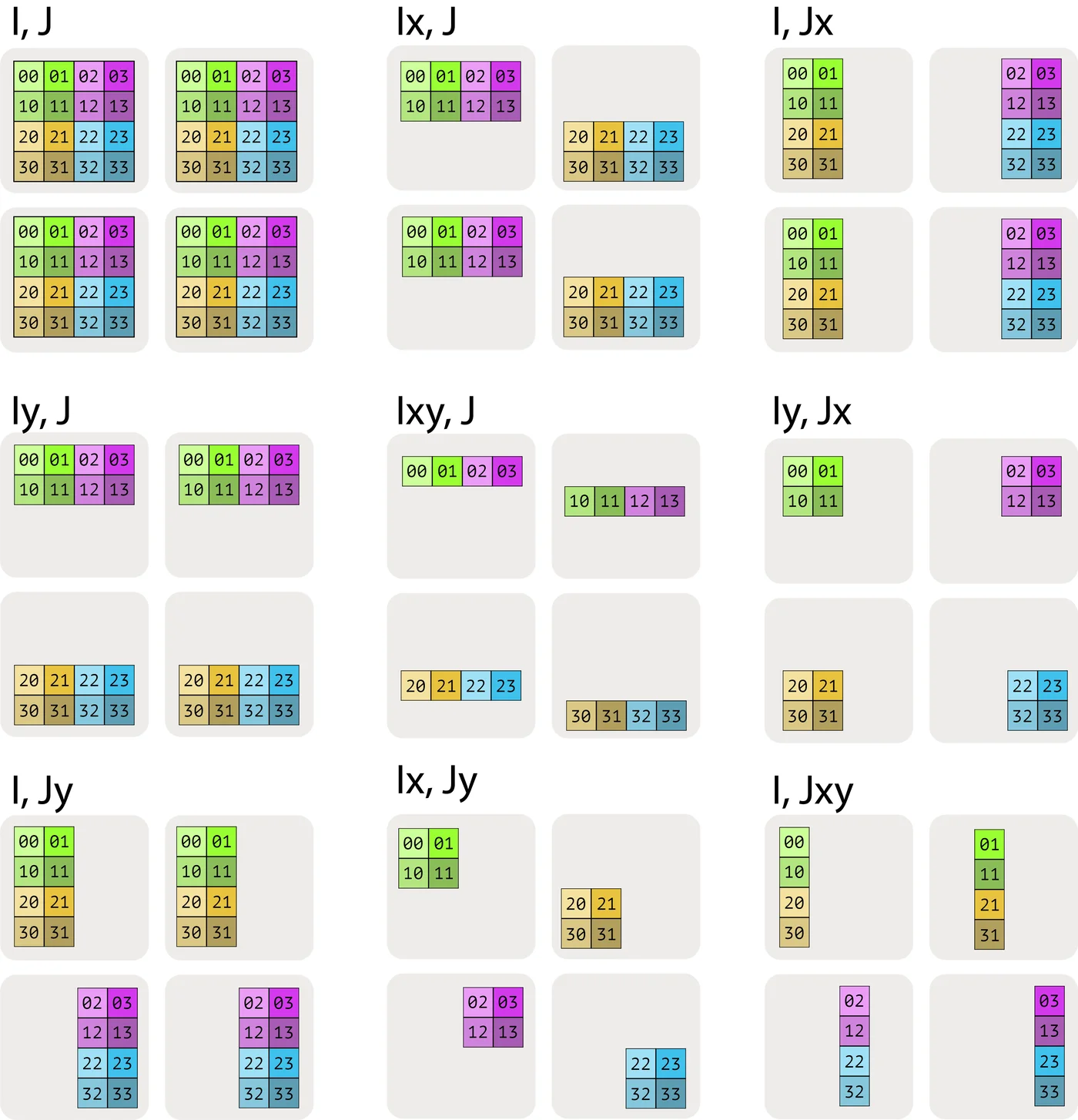Different sharding patterns Figure: Different sharding patterns visualized

Source: How to Scale Your Model

Rules and Constraints

  1. Unique Mesh Axis Assignment: A mesh axis can only be used once in a sharding (e.g., A[IX, JX] is invalid)
  2. Local Shape Calculation: For dimension I sharded across X: local_size = ⌈global_size / |X|⌉
  3. Memory Usage: Total memory across devices = global_size × replication_factor

Implementation in JAX

# Create a 2D mesh of 8 devices in a 4x2 grid
mesh = jax.make_mesh(axis_shapes=(4, 2), axis_names=('X', 'Y'))
 
# Define sharding specification
sharding = shd.NamedSharding(mesh, shd.PartitionSpec('X', 'Y'))
 
# Create a sharded array
A = jnp.ones((8192, 4096), dtype=jnp.bfloat16, device=sharding)

Benefits of Sharding

  1. Memory Efficiency: Enables working with arrays larger than a single device’s memory
  2. Computation Parallelism: Each device computes on a subset of the data
  3. Communication Reduction: Proper sharding can minimize data transfer between devices

Sharding Strategies

Different parallelism strategies use sharding in specific ways:

  • Data Parallelism: Shard batch dimension (A[BX, …])
  • Tensor Parallelism: Shard model dimensions (A[…, DX] or A[…, DX, FY])
  • Zero-1/2/3: Shard optimizer states, gradients, and/or parameters
  • Expert Parallelism: Shard expert dimension in Mixture of Experts models

Graph View